GPS−95でP.Misra, M.Pratt, B.Burke ＆ R.Ferranti：Adaptive Modeling of Receiver Clokfor Meter-Level DGPS Vertical Positioningとして報告され、その後、著者の一人P.MisraがGPSWorld誌の1996年4月号にThe Role oｆ ｔhe Clock in a GPS Receiverという若干解説的な記事を書いている。それらの概要は次の通りである。

GPSの測位では水平の測位の誤差に比べて高度の誤差は約1.5倍と大きく、その標準測位業務（SPS）の性能規格は2dmsの水平の位置精度は100mであるのに対して、垂直の精度は156mである。これは、測位に使用する衛星が、水平位置の場合は利用者の周囲に分布される場合が多いのに対して、垂直の高度の場合は衛星すべて利用者の上部にあって下部には衛星がないことによるからである。

GPSの測位は3次元の位置とともに利用者の受信機の中の時計の衛星の時計（GPS Time）に対するバイアスを4番目の未知数として、4次元、すなわち4衛星への疑似距離の測定によって行われる。もし、受信機の時計が完全に安定でGPS Timeに対するそのバイアスが精密に知れていれば、航法は3次元の位置のみについて求めることができる。

GPSによるrmsの位置誤差は次式で求められる：

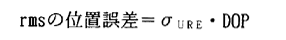
ここで、σUREは受信機の距離の測定値の誤差（利用者測距誤差）のrms値、DOPは受信機と衛星の幾何学特性である。この式でσUREは3次元と4次元の観測で同じ値をとるので、測位誤差はパラメータDOPによってのみ左右される。4次元の観測の場合のHDOPやVDOPの定義は観測行列（n×4）の項としてよく知られている。3次元の場合は、観測行列が（n×3）になり、HDOP3,VDOP3として区別する。

図3.3.2.4−1は24衛星配置のHDOP,VDOP,HDOP3とVDOP3の累積確率分布を示す。VDOPはHDOPより大きく、垂直位置誤差が水平位置誤差よりも大きいことの原因を示している。そのほか次が分かる。

（1）VDOP3は変化が少なく、VDOPよりも非常に小さく、HDOPよりも若干小さい。

（2）HDOP3とVDOP3の分布はほぼ等しい。

結論的に言うと、完全な時計を備えたGPSの利用者は、大きく改善されたDOPからの3次元の推定位置で、大きく改善された垂直位置の推定値が得られるだろう。

次に4次元測位での3次元の位置と時計のバイアスの関係を調べたのが図3.3.2.4-2である。この図は1日に亘って10秒置きにとった時計のバイアスの値と位置の誤差の関係を測定したものである。（a）は水平位置の誤差と時計のバイアスの誤差の関係であり、両者の関係は明らかではない。（b）は垂直位置の誤差と時計のバイアスの誤差の関係で、強い線形の相関を示している。

時計のバイアスの変化は疑似距離のすべてを変化させ、その変化量はすべてが等しい。利用者の高度の変化も疑似距離を変化させるが、その変化は一般には同じではなく、衛星の仰角がすべて同じであれば、利用者の高度の変化はすべての疑似距離を等しく変化させ前者との区別

前ページ　　　目次へ　　　次ページ